Compile-Time Graph

Abstract

CTGraph is a small C++17 project that implements a graph structure that can be used entirely at compile time. It started as just an experiment. I wanted to see just how much computation I can perform at compile time. I was heavily inspired by part of cpp_box. In there Jason Turner has managed to implement a compile-time finite state machine. I thought that Graphs are not too far off of a finite state machine so I decided to give the idea a try. I spend several days setting up the project and now it is a fully-fledged single header library. I still have not found any practical uses for CTGraph but for now, I am mainly developing it with educational propose. That is, I can discover a ton about C++ by programming smilingly useless things in it.

For more information as well as the source code, check out the GitHub page of the project.

Design goals

The project isn’t exactly serious but I’ve still defined several general guidelines around which I should design everything.

• Header only – the library mus be usable through the inclusion of a single header
• C++17 – once the header file of CTGraph is included, the source file must be compiled with C++17.
• Usable in constexpr context (mostly) – if all of the information is available at compile time, the functions of CTGraph should be able to produce their result also at compile-time. This is not that easy to pull off so I would allow myself a little bit of leniency here.
• Usable in const context (fully) – once the graph is defined, it should be fully usable through a const qualified reference to the object. This should be possible because the graph can’t be changed once defined so there is no reason for any method of the graph to modify the underlying structure.

Features so far

Basic graph definition

CTGraph requires the vertices of graph to be defines as a enumeration. For example, we can define the possible vertices like:

enum class NodeTypes
{
    UNKNOWN = 0,
    NODE_1 = 1,
    NODE_2 = 2,
    NODE_3 = 3,
    NODE_4 = 4,
    NODE_5 = 5,
    NODE_6 = 6,
    NODE_7 = 7
};

After that the definition of a graph is straight forward:

using namespace ctgraph;
static constexpr auto graph = Graph{Node{NodeTypes::NODE_1, NodeTypes::NODE_2, NodeTypes::NODE_3},
                                    Node{NodeTypes::NODE_2, NodeTypes::NODE_3, NodeTypes::NODE_4},
                                    Node{NodeTypes::NODE_3, NodeTypes::NODE_4},
                                    Node{NodeTypes::NODE_4},
                                    Node{NodeTypes::NODE_5, NodeTypes::NODE_6, NodeTypes::NODE_7}};

A Graph is defined through several Node objects. The semantics of the constructor of Node are Node{<vertex>, [<follower>]}. The first argument is the vertex to be added to the graph and the following vertices are the direct followers of the first one. To be noted is that only the vertices that come as a first argument of the Node constructor are considered “in” the graph. In the example, the will contain NODE_1, NODE_2, NODE_3, NODE_4 and NODE_5 as vertices but not NODE_6 and NODE_7.

The snippet defines the following graph: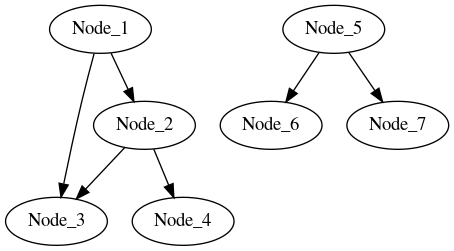

Accessing node

You can access the nth vertex through the get_node<n> method

constexpr auto node_0 = graph.get_node<0>(); // NodeTypes::NODE_1

Size of the graph

The number of vertices in the graph:

constexpr auto size = graph.size(); // 5

Checking if vertex is in the graph

The method contains can be used with any of the nodes define in the original enumeration:

constexpr bool is_node_4 = graph.contains(NodeTypes::NODE_4) // true
constexpr bool is_node_7 = graph.contains(NodeTypes::NODE_7) // false

Checking if two vertices are adjacent

Two node – n_1 and n_2 – are adjacent if and only if there is an edge n_1 -> n_2.

constexpr bool edge_2_3 = graph.adjacent(NodeTypes::NODE_2, NodeTypes::NODE_3) //true
constexpr bool edge_1_4 = graph.adjacent(NodeTypes::NODE_1, NodeTypes::NODE_4) //false

Accessing successors of a vertex

Accessing the nth successor of vertex can be done with the successor<n>(node) method:

constexpr auto node_1_succesor_0 = graph.successor<0>(NodeTypes::NODE_1);

Successors can also be accessed through a pointer ptr to the first one as well as their count c. It is guaranteed that the next c elements after ptr will be the successors of the given node:

constexpr auto num_succ = graph.count(NodeTypes::NODE_1); // 2
static constexpr auto ptr_succ = graph.followers(NodeTypes::NODE_1);
// *ptr_succ[0] == NodeTypes::NODE_2
// *ptr_succ[1] == NodeTypes::NODE_3
// *ptr_succ[3] - undefined behavior

There is also a convince function that return both the count and the pointer:

const auto[count, ptr] = get_successors(graph, NodeTypes::NODE_1);
// count == 2
// *ptr_succ[0] == NodeTypes::NODE_2
// *ptr_succ[1] == NodeTypes::NODE_3
// *ptr_succ[3] - undefined behavior